Poker Hand Scenarios
Typically, EV is used in call or fold scenarios. The EV of a fold is always $0, because however many times you run that same scenario, you are always going to win $0 when you fold. This, of course, is preferable to actually losing money, so the rule of thumb here is simple: when EV is negative, fold the hand; otherwise, make the call. In poker, players form sets of five playing cards, called hands, according to the rules of the game. Each hand has a rank, which is compared against the ranks of other hands participating in the showdown to decide who wins the pot. In high games, like Texas hold 'em and seven-card stud, the highest-ranking hands win. Poker Odds and Charts Chances of hitting, flopping and holding certain hands. These odds are a must know if you want to advance your game to a high level. For exact odds you can check out our poker hand odds calculator. We rounded the number to the nearest decimal for you. Looking for a challenging free poker quiz that blends the perfect mixture of strategy and interactive/fun? You’re in the right place! The goal with these quizzes and lessons is to give you a chance to put your poker knowledge to use.
Sanderson M. Smith
Home About Sanderson Smith Writings and Reflections Algebra 2 AP Statistics Statistics/Finance Forum
In many forms of poker, one is dealt 5 cards from astandard deck of 52 cards. The number of different 5 -card pokerhands is
A wonderful exercise involves having students verify probabilitiesthat appear in books relating to gambling. For instance, inProbabilities in Everyday Life, by John D. McGervey, one findsmany interesting tables containing probabilities for poker and othergames of chance.

This article and the tables below assume the reader is familiarwith the names for various poker hands. In the NUMBER OF WAYS columnof TABLE 2 are the numbers as they appear on page 132 in McGervey'sbook. I have done computations to verify McGervey's figures. Thiscould be an excellent exercise for students who are studyingprobability.
There are 13 denominations (A,K,Q,J,10,9,8,7,6,5,4,3,2) in thedeck. One can think of J as 11, Q as 12, and K as 13. Since an acecan be 'high' or 'low', it can be thought of as 14 or 1. With this inmind, there are 10 five-card sequences of consecutive dominations.These are displayed in TABLE 1.
TABLE 1The following table displays computations to verify McGervey'snumbers. There are, of course , many other possible poker handcombinations. Those in the table are specifically listed inMcGervey's book. The computations I have indicated in the table doyield values that are in agreement with those that appear in thebook.
N = NUMBER OF WAYS listed by McGervey | |||
Straight flush | There are four suits (spades, hearts, diamond, clubs). Using TABLE 1,4(10) = 40. | ||
Four of a kind | (13C1)(48C1) = 624. Choose 1 of 13 denominations to get four cards and combine with 1 card from the remaining 48. | ||
Full house | (13C1)(4C3)(12C1)(4C2) = 3,744. Choose 1 denominaiton, pick 3 of 4 from it, choose a second denomination, pick 2 of 4 from it. | ||
Flush | (4C1)(13C5) = 5,148. Choose 1 suit, then choose 5 of the 13 cards in the suit. This figure includes all flushes. McGervey's figure does not include straight flushes (listed above). Note that 5,148 - 40 = 5,108. | ||
Straight | (4C1)5(10) = 45(10) = 10,240 Using TABLE 1, there are 10 possible sequences. Each denomination card can be 1 of 4 in the denomination. This figure includes all straights. McGervey's figure does not include straight flushes (listed above). Note that 10,240 - 40 = 10,200. | ||
Three of a kind | (13C1)(4C3)(48C2) = 58,656. Choose 1 of 13 denominations, pick 3 of the four cards from it, then combine with 2 of the remaining 48 cards. This figure includes all full houses. McGervey's figure does not include full houses (listed above). Note that 54,912 - 3,744 = 54,912. | ||
Exactly one pair, with the pair being aces. | (4C2)(48C1)(44C1)(40C1)/3! = 84,480. Choose 2 of the four aces, pick 1 card from remaining 48 (and remove from consider other cards in that denomination), choose 1 card from remaining 44 (and remove other cards from that denomination), then chose 1 card from the remaining 40. The division by 3! = 6 is necessary to remove duplication in the choice of the last 3 cards. For instance, the process would allow for KQJ, but also KJQ, QKJ, QJK, JQK, and JKQ. These are the same sets of three cards, just chosen in a different order. | ||
Two pairs, with the pairs being 3's and 2's. | McGervey's figure excludes a full house with 3's and 2's. (4C2)(4C1)(44C1) = 1,584. Choose 2 of the 4 threes, 2 of the 4 twos, and one card from the 44 cards that are not 2's or 3's. |
'I must complain the cards are ill shuffled 'til Ihave a good hand.'
Poker Hand Scenarios Game
-Swift, Thoughts on Various Subjects
Home About Sanderson Smith Writings and Reflections Algebra 2 AP Statistics Statistics/Finance Forum

Previous Page Print This Page
Copyright © 2003-2009 Sanderson Smith
Poker Hand Scenarios Meaning
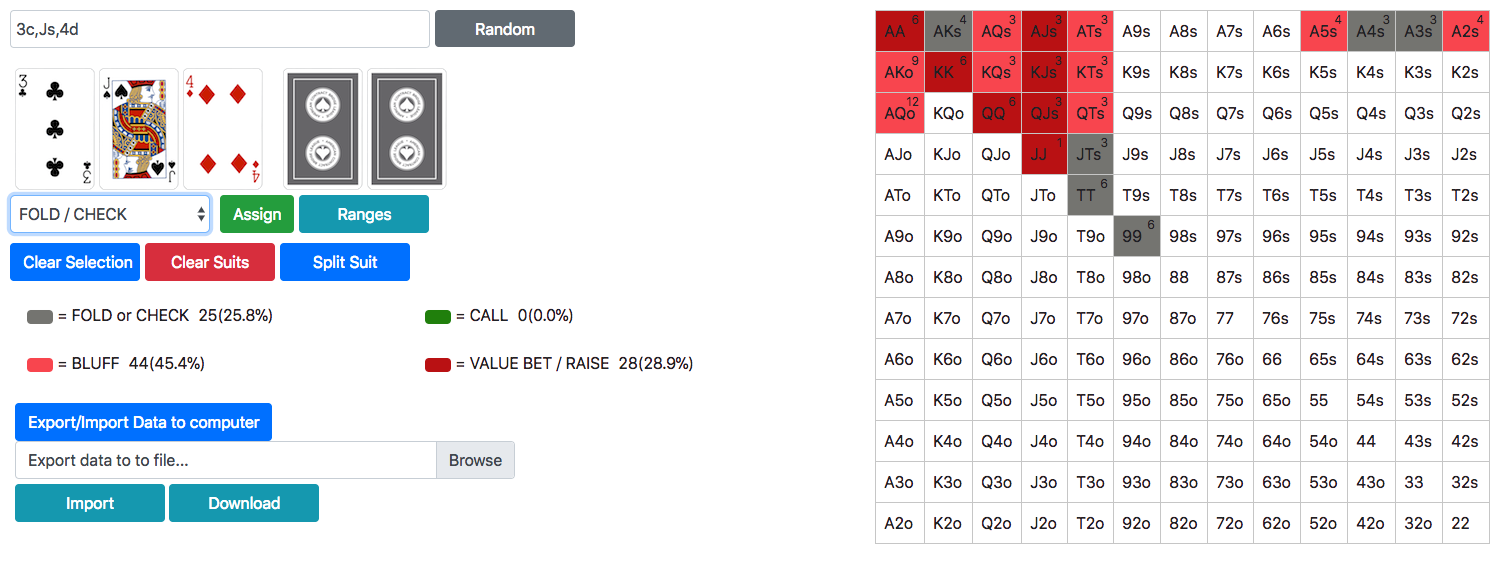
Online, free poker hand range calculator for everyone. The odds are instantly calculated and displayed as a card is added to the table or the dead card grid. Great tool for improving Texas Hold’em strategy.
Useful information regarding Poker Hand Range Calculator
What is range in Poker?
A range is a combination of hands a player might have at a given time. Thinking about what players have in the form of a range is valuable because it allows you to think about all of the possibilities of a hand. Experts say that once you understand the idea behind poker range you will soon forget the way of thinking earlier. Thanks to our calculator developed by Forest Turner now you can easily learn flop textures and how ranges split up on boards, how equities shift on turn and river cards.
What you can see with our Poker Hand Range calculator?
The Poker Hand Range Calculator instantly show equities, combination counts, and hand value breakdowns. Use the reset buttons to start over the calculation. First, we start with a preflop range. Get started by selecting a preflop range for the scenario you are analyzing.
What is the highest hand and hands order in poker?
You can see the hands order below starting with the highest ending with the lowest:
• RoyalFlush: 10, Jack, Queen, King, Ace all in the same suit.
• StraightFlush: Five cards in a row, all in the same suit.
• Four of aKind: The same card in each of the four suits.
• FullHouse: A pair plus three of a kind in the same hand.
• Flush:Five cards, all in one suit but no numerical order (4, 9, 10, King, Ace in onesuit).
• Straight:Five cards in numerical order, but no same suit (4, 5, 6, 7, 8 with differentsuit).
• Three ofa Kind: Three of one card (3 Queens).
• Two Pair:Two different pairings of the same card in one hand (two Aces and two Jacks forexample).
• One Pair: Two cards of the same card (twoAces for example).
• High Card: If you have nothing the highest card plays.